An autoencoder that differs from others (with deterministic encoder) by mapping each input $\mathbf{x}$ to a distribution over the possible values of the latent representation $\mathbf{z}$ from which $\mathbf{x}$ could have been generated.
Problem setup
Consider the following graphical model
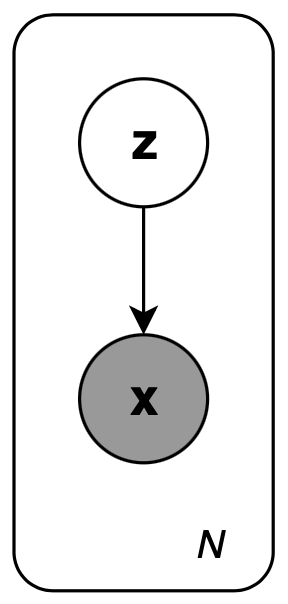
which consists of $N$ i.i.d samples $\mathbf{x}^{(1)},\ldots,\mathbf{x}^{(N)}$ and $N$ unobserved samples $\mathbf{z}^{(1)},\ldots,\mathbf{z}^{(N)}$. The generative process proceeds as:
- A value $\mathbf{z}^{(i)}$ is drawn from some prior distribution $\mathbf{z}\sim p_{\boldsymbol{\theta}^*}(\mathbf{z})$
- A datapoint $\mathbf{x}^{(i)}$ is generated from some conditional distribution $\mathbf{x}\sim p_{\boldsymbol{\theta}^*}(\mathbf{x}\vert\mathbf{z}=\mathbf{z}^{(i)})$
Consider the inference problem where we are interested in computing the posterior \begin{equation} p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x})=\frac{p_\boldsymbol{\theta}(\mathbf{x}\vert\mathbf{z})p_\boldsymbol{\theta}(\mathbf{z})}{p_\boldsymbol{\theta}(\mathbf{x})}=\frac{p_\boldsymbol{\theta}(\mathbf{x}\vert\mathbf{z})p_\boldsymbol{\theta}(\mathbf{z})}{\int p_\boldsymbol{\theta}(\mathbf{x}\vert\mathbf{z})p_\boldsymbol{\theta}(\mathbf{z})d\boldsymbol{\theta}} \end{equation} Unfortunately the integral of the marginal likelihood $p_\boldsymbol{\theta}(\mathbf{x})=\int p_\boldsymbol{\theta}(\mathbf{x}\vert\mathbf{z})p_\boldsymbol{\theta}(\mathbf{z})d\boldsymbol{\theta}$ is normally intractable, which would prevent us from computing the posterior efficiently. One potential solution is to approximate it with a tractable distribution $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$.
The variational bound
We have that the marginal likelihood $p_\boldsymbol{\theta}(\mathbf{x})=p_\boldsymbol{\theta}(\mathbf{x}^{(1)},\ldots,\mathbf{x}^{(N)})$ can be described via the marginal likelihoods of individual datapoints: \begin{equation} p_\boldsymbol{\theta}(\mathbf{x})=p_\boldsymbol{\theta}(\mathbf{x}^{(1)},\ldots,\mathbf{x}^{(N)})=\prod_{i=1}^{N}p_\boldsymbol{\theta}(\mathbf{x}^{(i)}) \end{equation} which implies that \begin{equation} \log p_\boldsymbol{\theta}(\mathbf{x})=\log p_\boldsymbol{\theta}(\mathbf{x}^{(1)},\ldots,\mathbf{x}^{(N)})=\sum_{i=1}^{N}\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)}) \end{equation} Consider the log-likelihood of the datapoint $i$, we have: \begin{align} \hspace{-1cm}\log p_\boldsymbol{\theta}({\mathbf{x}^{(i)}})&=\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)})\int q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})d\mathbf{z} \\ &=\int q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\log\frac{p_\boldsymbol{\theta}(x^{(i)},\mathbf{z})}{p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})}d\mathbf{z} \\ &=\int q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\log\left(\frac{p_\boldsymbol{\theta}(\mathbf{x}^{(i)},\mathbf{z})}{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\frac{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}{p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})}\right)d\mathbf{z} \\ &=D_\text{KL}\left(q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\big\Vert p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})\right)+\int q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\log\frac{p_\boldsymbol{\theta}(\mathbf{x}^{(i)},\mathbf{z})}{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}d\mathbf{z} \\ &=D_\text{KL}\left(q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\big\Vert p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})\right)+\underbrace{\mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[-\log q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})+\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)},\mathbf{z})\right]}_{\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})}, \end{align} where the first RHS term is the KL divergence of the approximate from the true posterior and the second RHS term, denoted as $\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})$, is referred as the (variational) lower bound, also known as the evidence lower bound (ELBO) on the marginal likelihood of datapoint $i$. The reason for this name is that, recalling that by Jensen’s inequality, the KL divergence is non-negative, we then have \begin{equation} \log p_\boldsymbol{\theta}(\mathbf{x}^{(i)})\geq\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})=\mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[-\log q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})+\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)},\mathbf{z})\right]\label{eq:tvb.1} \end{equation} We wish to find $\boldsymbol{\phi}^*$ such that for each datapoint $i$ the approximate $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})$ is as close to the true posterior $p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})$ as possible, which means: \begin{align} \boldsymbol{\phi}^*&=\underset{\boldsymbol{\phi}}{\text{argmin }}D_\text{KL}\left(q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\big\Vert p_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})\right) \\ &=\underset{\boldsymbol{\phi}}{\text{argmin}}\left[\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)})-\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})\right] \\ &=\underset{\boldsymbol{\phi}}{\text{argmax }}\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)}) \end{align} This variational lower bound can also be written as \begin{align} \mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})&=\mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[-\log q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})+\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)},\mathbf{z})\right] \\ &=\mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[-\log q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})+\log p_\boldsymbol{\theta}(\mathbf{z})+\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)}\vert\mathbf{z})\right] \\ &=-D_\text{KL}\left(q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\big\Vert p_\boldsymbol{\theta}(\mathbf{z})\right)+\mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)}\vert\mathbf{z})\right]\label{eq:tvb.2} \end{align} Hence, we wish to differentiate and optimize the ELBO $\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})$ w.r.t both the variational parameters $\boldsymbol{\phi}$ and generative parameters $\boldsymbol{\theta}$.
The reparameterization trick
Let $\mathbf{z}$ be a continuous r.v and $\mathbf{z}\sim q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ be some conditional distribution. Assume that we can express $\mathbf{z}$ as a deterministic variable $\mathbf{z}=g_\boldsymbol{\phi}(\mathbf{\epsilon},\mathbf{x})$ where $\boldsymbol{\epsilon}$ is an auxiliary variable with independent marginal $p(\boldsymbol{\epsilon})$, and $g_\boldsymbol{\phi}(\cdot)$ is some deterministic vector-valued function parameterized by $\boldsymbol{\theta}$.
The reparameterization trick allows us to sample $\mathbf{z}$ through $\boldsymbol{\epsilon}$: i.e. instead of sampling from $\mathbf{z}\sim q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$, we first sample $\boldsymbol{\epsilon}$ according to $p(\boldsymbol{\epsilon})$ then transform from $\boldsymbol{\epsilon}$ to $\mathbf{z}$ via $g_\boldsymbol{\phi}$.
For instance, the univariate Gaussian case: let $z\sim p(z\vert x)=\mathcal{N}(\mu,\sigma^2)$, which can be described as $z=\mu+\sigma\epsilon$ where $\epsilon\sim\mathcal{N}(0,1)$.
These are some choices of $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ with corresponding $g_\boldsymbol{\phi}(\cdot)$ and $p(\boldsymbol{\epsilon})$ on which we can use the reparameterization trick:
- $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ is a tractable inverse CDF; $\boldsymbol{\epsilon}\sim\text{Unif}(\mathbf{0},\mathbf{I})$ and $g_\boldsymbol{\phi}(\boldsymbol{\epsilon},\mathbf{x})$ is the inverse CDF of $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$. E.g. Exponential, Cauchy, Logistic, Rayleigh, Pareto, Weibull, Reciprocal, Gompertz, Gumbel and Erlang distributions.
- Similar to the above example, for any "location-scale" family of distributions we can choose the standard distribution (location $\mu=0$, scale $\sigma=1$) as the auxiliary variable $\boldsymbol{\epsilon}$ and let $g(\cdot)=\mu+\sigma\boldsymbol{\epsilon}$. E.g. Laplace, Elliptical, Student's t, Logistic, Uniform, Triangular and Gaussian distributions.
- $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ is a composition. E.g. Log-normal (exponentiation of Normal r.v), Gamma (sum of exponentially distributed r.v.s), Dirichlet (weighted sum of Gamma variates), Beta, Chi-squared and F distributions.
The SGVB estimator
For an approximate posterior $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ satisfying one of the above conditions, we can reparameterize the r.v $\tilde{\mathbf{z}}\sim q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ using a differentiable transformation $g_\boldsymbol{\phi}(\boldsymbol{\epsilon},\mathbf{x})$ of an auxiliary variable $\boldsymbol{\epsilon}$: \begin{equation} \tilde{\mathbf{z}}=g_\boldsymbol{\phi}(\boldsymbol{\epsilon},\mathbf{x}),\hspace{1cm}\boldsymbol{\epsilon}\sim p(\boldsymbol{\epsilon}) \end{equation} Consider some function $f(\mathbf{z})$, we have \begin{equation} \mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[f(\mathbf{z})\right]=\mathbb{E}_{p(\boldsymbol{\epsilon})}\left[f(g_\boldsymbol{\phi}(\boldsymbol{\epsilon},\mathbf{x}^{(i)}))\right], \end{equation} which then can be estimated by Monte Carlo method w.r.t $p(\boldsymbol{\epsilon})$. Specifically, \begin{equation} \mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[f(\mathbf{z})\right]=\mathbb{E}_{p(\boldsymbol{\epsilon})}\left[f(g_\boldsymbol{\phi}(\boldsymbol{\epsilon},\mathbf{x}^{(i)}))\right]\simeq\frac{1}{L}\sum_{l=1}^{L}f(g_\boldsymbol{\phi}(\boldsymbol{\epsilon}^{(l)},\mathbf{x}^{(i)})), \end{equation} where $\boldsymbol{\epsilon}^{(l)}\sim p(\boldsymbol{\epsilon})$. Applying this to the variational lower bound \eqref{eq:tvb.1} yields the generic Stochastic Gradient Variational Bayes (SGVB) estimator $\tilde{\mathcal{L}}^A(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})\simeq\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})$: \begin{equation} \tilde{\mathcal{L}}^A(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})=\frac{1}{L}\sum_{l=1}^{L}\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)},\mathbf{z}^{(i,l)})-\log q_\boldsymbol{\phi}(\mathbf{z}^{(i,l)}\vert\mathbf{x}^{(i)}), \end{equation} where $\mathbf{z}^{(i,l)}=g_\boldsymbol{\phi}(\boldsymbol{\epsilon}^{(i,l)},\mathbf{x}^{(i)})$ and $\boldsymbol{\epsilon}^{(l)}\sim p(\boldsymbol{\epsilon})$.
Considering the other form of the ELBO given in \eqref{eq:tvb.2}, the KL divergence $D_\text{KL}\left(q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\Vert p_\boldsymbol{\theta}(\mathbf{z})\right)$ can be often integrated analytically, such that only the expected reconstruction error $\mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})}\left[\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)}\vert\mathbf{z})\right]$ requires estimation by sampling. This gives rise to the second version of the SGVB estimator $\tilde{\mathcal{L}}^B(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})\simeq\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})$, corresponding to \eqref{eq:tvb.2}, which typically has less variance than the generic one: \begin{equation} \tilde{\mathcal{L}}^B(\boldsymbol{\theta},\boldsymbol{\phi};\mathbf{x}^{(i)})=-D_\text{KL}\left(q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\big\Vert p_\boldsymbol{\theta}(\mathbf{z})\right)+\frac{1}{L}\sum_{l=1}^{L}\log p_\boldsymbol{\theta}(\mathbf{x}^{(i)}\vert\mathbf{z}^{(i,l)}), \end{equation} where $\mathbf{z}^{(i,l)}=g_\boldsymbol{\phi}(\boldsymbol{\epsilon}^{(i,l)},\mathbf{x}^{(i)})$ and $\boldsymbol{\epsilon}\sim p(\boldsymbol{\epsilon})$.
Variational Autoencoder
Autoencoders are neural networks designed to learn an identity function in an unsupervised manner to reconstruct the original input while compressing the data in the process in order to discover a more efficient and compressed representation. Specifically, it uses an encoder, $f_\boldsymbol{\phi}$, parameterized by $\boldsymbol{\phi}$ to map inputs $\mathbf{x}$ to a low-dimensional latent space, $\mathbf{z}=f_\boldsymbol{\phi}(\mathbf{x})$ and then tries to reconstruct the inputs using a decoder, $g_\boldsymbol{\theta}$, $\mathbf{x}’=g_\boldsymbol{\theta}(\mathbf{z})=g_\boldsymbol{\theta}(f_\boldsymbol{\phi}(\mathbf{x}))$.
The parameters $\boldsymbol{\phi},\boldsymbol{\theta}$ are trained jointly with the goal is to reconstruct the original input, $\mathbf{x}\approx g_\boldsymbol{\theta}(f_\boldsymbol{\phi}(\mathbf{x}))$. In other words, it tries to minimize the “distance” between the original input and the sample output. For instance, it could use MSE as the distance metric while attempting to minimize the loss function: \begin{equation} \mathcal{L}(\boldsymbol{\phi},\boldsymbol{\theta})=\big\Vert\mathbf{x}-g_\boldsymbol{\theta}(f_\boldsymbol{\phi}(\mathbf{x}))\big\Vert_2^2 \end{equation}
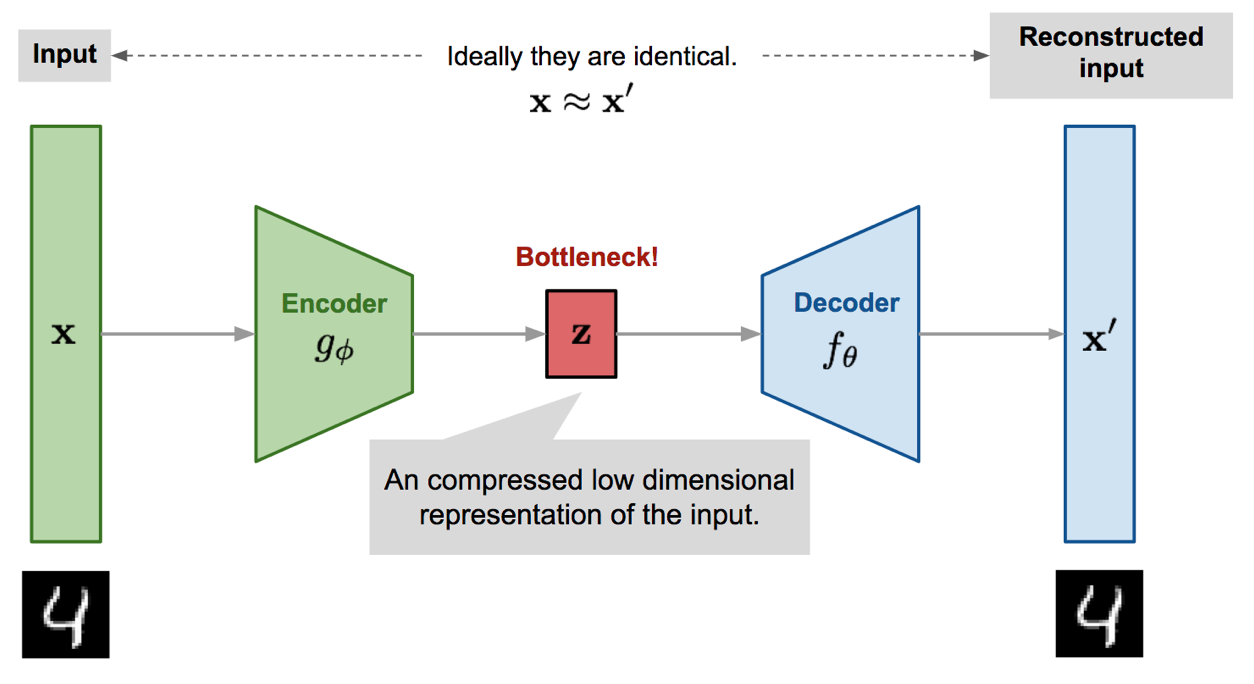
If we use neural networks to represent both the approximate posterior $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ and the likelihood $p_\boldsymbol{\theta}(\mathbf{x}\vert\mathbf{z})$, we end up with an autoencoder called variational autoencoder or VAE. Specifically,
- The recognition model $q_\boldsymbol{\phi}(\mathbf{z}\vert\mathbf{x})$ is considered a probabilistic encoder, since given a datapoint $\mathbf{x}$ it produces a distribution over the possible values of the latent representation $\mathbf{z}$ from which $\mathbf{x}$ could have been generated.
- The likelihood $p_\boldsymbol{\theta}(\mathbf{x}\vert\mathbf{z})$ is referred as a probabilistic decoder, since given a latent vector $\mathbf{z}$ it produces a distribution over the possible values of $\mathbf{x}$.
- In learning variational parameters $\boldsymbol{\phi}$ and generative parameters $\boldsymbol{\theta}$, the goal is to minimize the loss function, which is the negative of the variational lower bound $\mathcal{L}(\boldsymbol{\phi},\boldsymbol{\theta};\mathbf{x})$.
To be more specific, considering the ELBO on the marginal likelihood of a datapoint $i$ given in \eqref{eq:tvb.2}, the first term, $D_\text{KL}(q_\boldsymbol{\theta}(\mathbf{z}\vert\mathbf{x}^{(i)})\Vert p_\boldsymbol{\theta}(\mathbf{z}))$, acts as a regularizer, while the second term, the expected log-likelihood, is the reconstruction loss, which encourages the decoder to reconstruct the data.
Preferences
[1] Diederik P. Kingma, Max Welling. Auto-Encoding Variational Bayes. arXiv preprint, arXiv:1312.6114, 2013.
[2] Kevin P. Murphy. Probabilistic Machine Learning: Advanced Topics. The MIT Press, 2023.
[3] Lilian Weng. From Autoencoder to Beta-VAE. lilianweng.github.io, 2018.